Hype, hope, and modern science fiction cinema have captured our imaginations and created significant expectations around the deployment of machine learning and AI in commercially available products in our near future (e.g. self driving cars). However, don’t expect to be transported to Machine City in Matrix Revolutions (very cool, in its own way) any time soon. The rise of the machines will have to wait. Expect to see plenty more incremental steps such as collision avoidance and semi-autonomous driving (hopefully, with limited significant human cost as we adjust to the reality of the state of the technology today… see – tesla on autopilot slams into parked firetruck), and a few eye catching advances such as Amazon Go (how cool is that!?).
At least some of the public attention on deep learning is from the name, aided by some great science fiction filmmaking and computer graphics, evoking images of an inward looking, thoughtful, mathematically robust, and far less bloody, Ex Machina thing.
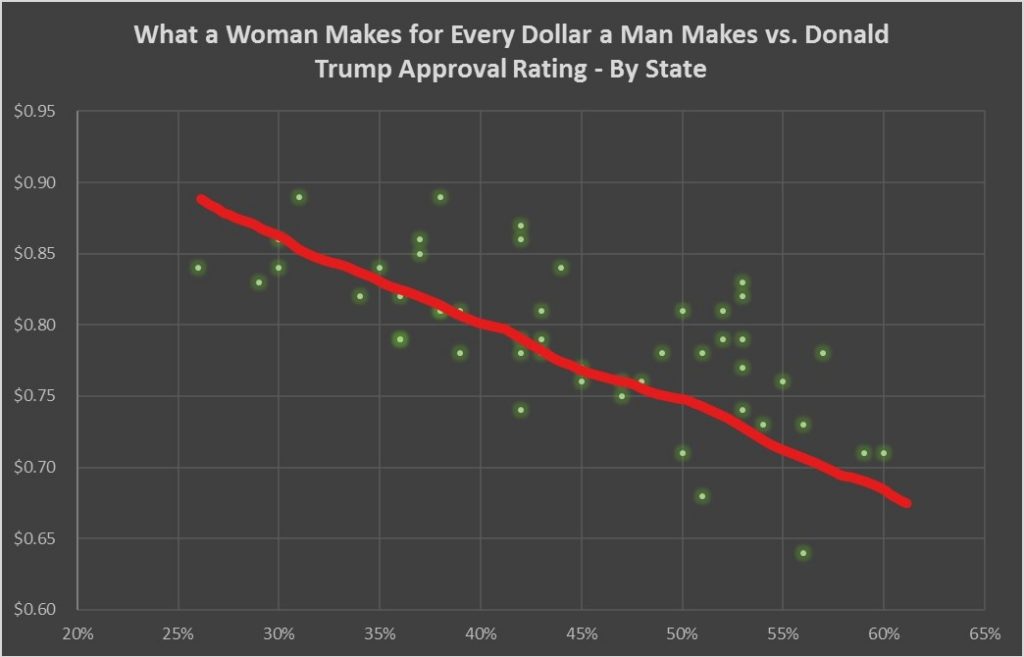
The underlying concept of deep learning, however, is not quite that deep. In fact, it is conceptually very similar to simple regression analysis, which evaluates and describes a relationship between variables – say between gender wage gap and Donald Trump’s popularity (true story).
Sources: National Women’s Law Center, Gallup
The typical way to try and describe this type of relationship is to fit a straight line on the data that best summarizes the relationship. Why often a straight line? Well, computationally a straight-line relationship is easiest to try and fit. Similar ease of computation considerations are true for deep learning models as well.
A major consideration is to decide what line best fits the data. We choose a line from options that minimizes an aggregate measure of difference between the actual data to that predicted by the line – the line of best fit. That is the essence of deep learning – computational techniques, albeit far more complicated, that try and establish relationships between variables by minimizing some measure of error.
A key difference is that deep learning tests out relationships using additional layers of variables. Hence the term “deep”. More layers = deep. We do not make any assumption on what these variables are, just how many layers, the number of variables in each layer, and the mathematical relationship between the layers (parallel to the example of a straight-line relationship above). There is no magic to these choices. You select a configuration based on what is computationally feasible and provides the best results, and then you have deep learning. Still some ways away from Machine City.